Smogseer training at 100 epochs

In [1]:

import matplotlib.pyplot as plt
import xarray as xr
import numpy as np
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.impute import SimpleImputer
from tensorflow.keras.models import load_model
import matplotlib.pyplot as plt
from tensorflow.keras.utils import Sequence

In [2]:

# Load your dataset
ds = xr.open_dataset('S5PL2_5D.nc')
ds

<xarray.Dataset> Size: 2GB
Dimensions:         (time: 366, lat: 291, lon: 512, bnds: 2)
Coordinates:
  * lat             (lat) float64 2kB 34.36 34.33 34.3 ... 24.97 24.94 24.9
  * lon             (lon) float64 4kB 68.15 68.19 68.22 ... 84.75 84.79 84.82
  * time            (time) datetime64[ns] 3kB 2019-01-03T12:00:00 ... 2024-01...
    time_bnds       (time, bnds) datetime64[ns] 6kB ...
Dimensions without coordinates: bnds
Data variables:
    AER_AI_340_380  (time, lat, lon) float32 218MB ...
    AER_AI_354_388  (time, lat, lon) float32 218MB ...
    CH4             (time, lat, lon) float32 218MB ...
    CLOUD_FRACTION  (time, lat, lon) float32 218MB ...
    CO              (time, lat, lon) float32 218MB ...
    HCHO            (time, lat, lon) float32 218MB ...
    NO2             (time, lat, lon) float32 218MB ...
    O3              (time, lat, lon) float32 218MB ...
    SO2             (time, lat, lon) float32 218MB ...
Attributes:
    Conventions:               CF-1.7
    title:                     S5PL2 Data Cube Subset
    history:                   [{'program': 'xcube_sh.chunkstore.SentinelHubC...
    date_created:              2024-05-02T13:00:01.155492
    time_coverage_start:       2019-01-01T00:00:00+00:00
    time_coverage_end:         2024-01-05T00:00:00+00:00
    time_coverage_duration:    P1830DT0H0M0S
    time_coverage_resolution:  P5DT0H0M0S
    geospatial_lon_min:        68.137207
    geospatial_lat_min:        24.886436
    geospatial_lon_max:        84.836426
    geospatial_lat_max:        34.37759367382812

xarray.Dataset

• Dimensions:
  • time: 366
  • lat: 291
  • lon: 512
  • bnds: 2
• Coordinates: (4)
  • lat
    (lat)
    float64
    34.36 34.33 34.3 ... 24.94 24.9

    units :

    decimal_degrees

    long_name :

    latitude

    standard_name :

    latitude

    array([34.361286, 34.32867 , 34.296055, ..., 24.967975, 24.935359, 24.902744])

  • lon
    (lon)
    float64
    68.15 68.19 68.22 ... 84.79 84.82

    units :

    decimal_degrees

    long_name :

    longitude

    standard_name :

    longitude

    array([68.153515, 68.18613 , 68.218746, ..., 84.754887, 84.787503, 84.820118])

  • time
    (time)
    datetime64[ns]
    2019-01-03T12:00:00 ... 2024-01-...

    standard_name :

    time

    bounds :

    time_bnds

    array(['2019-01-03T12:00:00.000000000', '2019-01-08T12:00:00.000000000',
           '2019-01-13T12:00:00.000000000', ..., '2023-12-23T12:00:00.000000000',
           '2023-12-28T12:00:00.000000000', '2024-01-02T12:00:00.000000000'],
          dtype='datetime64[ns]')

  • time_bnds
    (time, bnds)
    datetime64[ns]
    ...

    [732 values with dtype=datetime64[ns]]

• Data variables: (9)
  • AER_AI_340_380
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    Unitless

    [54531072 values with dtype=float32]

  • AER_AI_354_388
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    Unitless

    [54531072 values with dtype=float32]

  • CH4
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    parts per billion

    [54531072 values with dtype=float32]

  • CLOUD_FRACTION
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    Unitless

    [54531072 values with dtype=float32]

  • CO
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    mol/m^2

    [54531072 values with dtype=float32]

  • HCHO
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    mol/m^2

    [54531072 values with dtype=float32]

  • NO2
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    mol/m^2

    [54531072 values with dtype=float32]

  • O3
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    mol/m^2

    [54531072 values with dtype=float32]

  • SO2
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    mol/m^2

    [54531072 values with dtype=float32]

• Indexes: (3)
  • lat
    PandasIndex

    PandasIndex(Index([34.361285842773434,  34.32867018066406,  34.29605451855468,
            34.26343885644531,  34.23082319433593,  34.19820753222656,
            34.16559187011718,  34.13297620800781,  34.10036054589843,
            34.06774488378906,
           ...
            25.19628479003906, 25.163669127929687,  25.13105346582031,
           25.098437803710937,  25.06582214160156, 25.033206479492186,
            25.00059081738281, 24.967975155273436,  24.93535949316406,
           24.902743831054686],
          dtype='float64', name='lat', length=291))

  • lon
    PandasIndex

    PandasIndex(Index([ 68.1535148310547, 68.18613049316407, 68.21874615527344,
           68.25136181738281,  68.2839774794922, 68.31659314160157,
           68.34920880371094, 68.38182446582032,  68.4144401279297,
           68.44705579003907,
           ...
           84.52657720996093, 84.55919287207031, 84.59180853417969,
           84.62442419628906, 84.65703985839843, 84.68965552050781,
           84.72227118261719, 84.75488684472657, 84.78750250683593,
           84.82011816894531],
          dtype='float64', name='lon', length=512))

  • time
    PandasIndex

    PandasIndex(DatetimeIndex(['2019-01-03 12:00:00', '2019-01-08 12:00:00',
                   '2019-01-13 12:00:00', '2019-01-18 12:00:00',
                   '2019-01-23 12:00:00', '2019-01-28 12:00:00',
                   '2019-02-02 12:00:00', '2019-02-07 12:00:00',
                   '2019-02-12 12:00:00', '2019-02-17 12:00:00',
                   ...
                   '2023-11-18 12:00:00', '2023-11-23 12:00:00',
                   '2023-11-28 12:00:00', '2023-12-03 12:00:00',
                   '2023-12-08 12:00:00', '2023-12-13 12:00:00',
                   '2023-12-18 12:00:00', '2023-12-23 12:00:00',
                   '2023-12-28 12:00:00', '2024-01-02 12:00:00'],
                  dtype='datetime64[ns]', name='time', length=366, freq=None))

• Attributes: (12)

  Conventions :

  CF-1.7

  title :

  S5PL2 Data Cube Subset

  history :

  [{'program': 'xcube_sh.chunkstore.SentinelHubChunkStore', 'cube_config': {'dataset_name': 'S5PL2', 'band_names': ['NO2', 'SO2', 'O3', 'CO', 'CH4', 'HCHO', 'AER_AI_340_380', 'AER_AI_354_388', 'CLOUD_FRACTION'], 'band_fill_values': None, 'band_sample_types': None, 'band_units': None, 'tile_size': [512, 291], 'bbox': [68.137207, 24.886436, 84.836426, 34.37759367382812], 'spatial_res': 0.032615662109375, 'crs': 'WGS84', 'upsampling': 'BILINEAR', 'downsampling': 'NEAREST', 'mosaicking_order': 'mostRecent', 'time_range': ['2019-01-01T00:00:00+00:00', '2023-12-31T00:00:00+00:00'], 'time_period': '5 days 00:00:00', 'time_tolerance': None, 'collection_id': None, 'four_d': False}}]

  date_created :

  2024-05-02T13:00:01.155492

  time_coverage_start :

  2019-01-01T00:00:00+00:00

  time_coverage_end :

  2024-01-05T00:00:00+00:00

  time_coverage_duration :

  P1830DT0H0M0S

  time_coverage_resolution :

  P5DT0H0M0S

  geospatial_lon_min :

  68.137207

  geospatial_lat_min :

  24.886436

  geospatial_lon_max :

  84.836426

  geospatial_lat_max :

  34.37759367382812

In [3]:

# Stack the features into a single DataArray
features = ['SO2', 'NO2', 'CH4', 'O3', 'CO', 'HCHO']
data = xr.concat([ds[feature] for feature in features], dim='feature')
data = data.transpose('time', 'lat', 'lon', 'feature')

# Convert to NumPy arrays
X_data = data.values.astype(np.float32)

# Normalize the input data
scaler = StandardScaler()
X_data = scaler.fit_transform(X_data.reshape(-1, X_data.shape[-1])).reshape(X_data.shape)

# Impute nan values with the mean of the respective feature
X_data_reshaped = X_data.reshape(-1, X_data.shape[-1])
imputer = SimpleImputer(strategy='mean')
X_data_imputed = imputer.fit_transform(X_data_reshaped)
X_data_imputed = X_data_imputed.reshape(X_data.shape)

# Add the time dimension to the input data
X_data_imputed = np.expand_dims(X_data_imputed, axis=1)

# Load your actual target data
ds_target = xr.open_dataset('S5PL2_5D.nc')
target_data = ds_target['AER_AI_340_380'].values.astype(np.float32)

# Normalize target data to [0, 1]
target_scaler = MinMaxScaler()
target_data = target_scaler.fit_transform(target_data.reshape(-1, 1)).reshape(target_data.shape)

# Impute nan values in target data
target_data_reshaped = target_data.reshape(-1, target_data.shape[-1])
target_data_imputed = imputer.fit_transform(target_data_reshaped)
target_data_imputed = target_data_imputed.reshape(target_data.shape)

# Ensure the target data shape is (num_samples, num_timesteps, num_latitudes, num_longitudes, 1)
target_data_imputed = target_data_imputed.reshape((target_data.shape[0], 1, target_data.shape[1], target_data.shape[2], 1))

# Remove samples with nan values in target data
non_nan_target_indices = ~np.isnan(target_data_imputed).any(axis=(1, 2, 3, 4))
X_data_clean = X_data_imputed[non_nan_target_indices]
y_data_clean = target_data_imputed[non_nan_target_indices]

# Ensure target values are within the valid range [0, 1]
print("Target data range: ", y_data_clean.max(), y_data_clean.min())

# Split data into training and validation sets
split_ratio = 0.8
split_idx = int(split_ratio * X_data_clean.shape[0])

X_train, X_val = X_data_clean[:split_idx], X_data_clean[split_idx:]
y_train, y_val = y_data_clean[:split_idx], y_data_clean[split_idx:]

Target data range:  1.0 0.0

In [4]:

print("Input shape:", X_data_clean.shape)
print("Target shape:", y_data_clean.shape)
print("Max and Min of Target Data:", y_data_clean.max(), y_data_clean.min())

Input shape: (366, 1, 291, 512, 6)
Target shape: (366, 1, 291, 512, 1)
Max and Min of Target Data: 1.0 0.0

In [5]:

print("Training data shape:", X_train.shape)
print("Validation data shape:", X_val.shape)
print("Training target shape:", y_train.shape)
print("Validation target shape:", y_val.shape)

Training data shape: (292, 1, 291, 512, 6)
Validation data shape: (74, 1, 291, 512, 6)
Training target shape: (292, 1, 291, 512, 1)
Validation target shape: (74, 1, 291, 512, 1)

In [6]:

import matplotlib.pyplot as plt

# Visualize a sample from the training data
sample_index = 0
plt.imshow(X_train[sample_index, 0, :, :, 2], cmap='viridis')
plt.title('Sample Input')
plt.show()

plt.imshow(y_train[sample_index, 0, :, :, 0], cmap='viridis')
plt.title('Sample Target')
plt.show()

In [31]:

np.save("X_val.npy", X_val)
np.save("Y_val.npy", y_val)

In [7]:

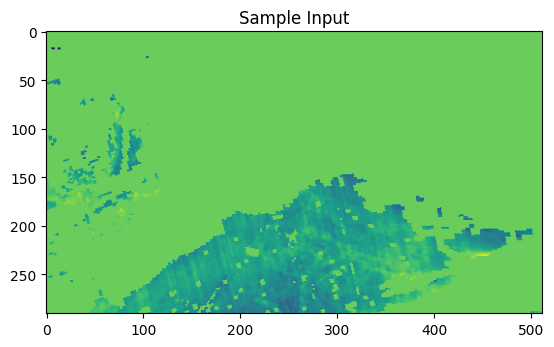
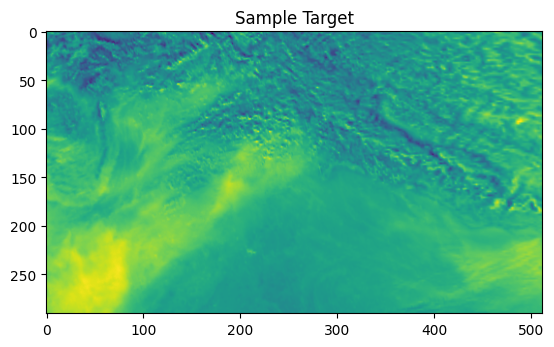
# Define the model with correct input shape
inp = layers.Input(shape=(1, X_data_clean.shape[2], X_data_clean.shape[3], X_data_clean.shape[4]))

x = layers.BatchNormalization()(inp)
x = layers.ConvLSTM2D(
    filters=16,
    kernel_size=(3, 3),
    padding="same",
    return_sequences=True,
    activation="tanh",
    recurrent_activation="sigmoid",
    kernel_initializer="glorot_uniform"
)(x)
x = layers.BatchNormalization()(x)
x = layers.ConvLSTM2D(
    filters=32,
    kernel_size=(3, 3),
    padding="same",
    return_sequences=True,
    activation="tanh",
    recurrent_activation="sigmoid",
    kernel_initializer="glorot_uniform"
)(x)
x = layers.BatchNormalization()(x)
x = layers.Conv3D(
    filters=1, kernel_size=(3, 3, 3), activation="sigmoid", padding="same"
)(x)

model = keras.models.Model(inp, x, name="smogseer")

# Use a reduced learning rate and gradient clipping
optimizer = keras.optimizers.Adam(learning_rate=1e-5, clipnorm=1.0)
model.compile(
    loss=keras.losses.binary_crossentropy,
    optimizer=optimizer,
    metrics=['mean_squared_error']
)

# Print the model summary
model.summary()

# Data Generator Class

class DataGenerator(Sequence):
    def __init__(self, X_data, y_data, batch_size):
        self.X_data = X_data
        self.y_data = y_data
        self.batch_size = batch_size
        self.indices = np.arange(X_data.shape[0])
        
    def __len__(self):
        return int(np.ceil(len(self.indices) / self.batch_size))
    
    def __getitem__(self, index):
        batch_indices = self.indices[index * self.batch_size:(index + 1) * self.batch_size]
        batch_X = self.X_data[batch_indices]
        batch_y = self.y_data[batch_indices]
        return batch_X, batch_y

    def on_epoch_end(self):
        np.random.shuffle(self.indices)

batch_size = 1
train_generator = DataGenerator(X_train, y_train, batch_size)
val_generator = DataGenerator(X_val, y_val, batch_size)

# Define callbacks for monitoring and adjusting learning rate
callbacks = [
    keras.callbacks.ReduceLROnPlateau(
        monitor='val_loss', factor=0.1, patience=10, verbose=1, min_lr=1e-7
    ),
    keras.callbacks.EarlyStopping(
        monitor='val_loss', patience=15, verbose=1, restore_best_weights=True
    ),
    keras.callbacks.TensorBoard(log_dir='./logs')
]

# Train the model using data generators
history = model.fit(train_generator, epochs=100, validation_data=val_generator, callbacks=callbacks)
# Save the model
model.save('smogseer.keras')

Model: "smogseer"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ input_layer (InputLayer)        │ (None, 1, 291, 512, 6) │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ batch_normalization             │ (None, 1, 291, 512, 6) │            24 │
│ (BatchNormalization)            │                        │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv_lstm2d (ConvLSTM2D)        │ (None, 1, 291, 512,    │        12,736 │
│                                 │ 16)                    │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ batch_normalization_1           │ (None, 1, 291, 512,    │            64 │
│ (BatchNormalization)            │ 16)                    │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv_lstm2d_1 (ConvLSTM2D)      │ (None, 1, 291, 512,    │        55,424 │
│                                 │ 32)                    │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ batch_normalization_2           │ (None, 1, 291, 512,    │           128 │
│ (BatchNormalization)            │ 32)                    │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv3d (Conv3D)                 │ (None, 1, 291, 512, 1) │           865 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

 Total params: 69,241 (270.47 KB)

 Trainable params: 69,133 (270.05 KB)

 Non-trainable params: 108 (432.00 B)

Epoch 1/100

c:\Users\khant\Documents\smogseer\venv\lib\site-packages\keras\src\trainers\data_adapters\py_dataset_adapter.py:121: UserWarning: Your `PyDataset` class should call `super().__init__(**kwargs)` in its constructor. `**kwargs` can include `workers`, `use_multiprocessing`, `max_queue_size`. Do not pass these arguments to `fit()`, as they will be ignored.
  self._warn_if_super_not_called()

292/292 ━━━━━━━━━━━━━━━━━━━━ 143s 472ms/step - loss: 0.7290 - mean_squared_error: 0.1448 - val_loss: 0.6891 - val_mean_squared_error: 0.1320 - learning_rate: 1.0000e-05
Epoch 2/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 469ms/step - loss: 0.7017 - mean_squared_error: 0.1329 - val_loss: 0.6959 - val_mean_squared_error: 0.1347 - learning_rate: 1.0000e-05
Epoch 3/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 136s 466ms/step - loss: 0.6911 - mean_squared_error: 0.1275 - val_loss: 0.6945 - val_mean_squared_error: 0.1335 - learning_rate: 1.0000e-05
Epoch 4/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 474ms/step - loss: 0.6827 - mean_squared_error: 0.1240 - val_loss: 0.6839 - val_mean_squared_error: 0.1284 - learning_rate: 1.0000e-05
Epoch 5/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 136s 466ms/step - loss: 0.6741 - mean_squared_error: 0.1198 - val_loss: 0.6764 - val_mean_squared_error: 0.1248 - learning_rate: 1.0000e-05
Epoch 6/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 141s 482ms/step - loss: 0.6639 - mean_squared_error: 0.1150 - val_loss: 0.6625 - val_mean_squared_error: 0.1180 - learning_rate: 1.0000e-05
Epoch 7/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 150s 513ms/step - loss: 0.6518 - mean_squared_error: 0.1083 - val_loss: 0.6491 - val_mean_squared_error: 0.1114 - learning_rate: 1.0000e-05
Epoch 8/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 153s 523ms/step - loss: 0.6380 - mean_squared_error: 0.1018 - val_loss: 0.6330 - val_mean_squared_error: 0.1035 - learning_rate: 1.0000e-05
Epoch 9/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 143s 488ms/step - loss: 0.6223 - mean_squared_error: 0.0940 - val_loss: 0.6140 - val_mean_squared_error: 0.0941 - learning_rate: 1.0000e-05
Epoch 10/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 474ms/step - loss: 0.6055 - mean_squared_error: 0.0856 - val_loss: 0.5990 - val_mean_squared_error: 0.0868 - learning_rate: 1.0000e-05
Epoch 11/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 474ms/step - loss: 0.5873 - mean_squared_error: 0.0776 - val_loss: 0.5783 - val_mean_squared_error: 0.0768 - learning_rate: 1.0000e-05
Epoch 12/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.5693 - mean_squared_error: 0.0687 - val_loss: 0.5591 - val_mean_squared_error: 0.0677 - learning_rate: 1.0000e-05
Epoch 13/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 473ms/step - loss: 0.5517 - mean_squared_error: 0.0597 - val_loss: 0.5410 - val_mean_squared_error: 0.0591 - learning_rate: 1.0000e-05
Epoch 14/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 145s 497ms/step - loss: 0.5337 - mean_squared_error: 0.0515 - val_loss: 0.5243 - val_mean_squared_error: 0.0514 - learning_rate: 1.0000e-05
Epoch 15/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 142s 488ms/step - loss: 0.5173 - mean_squared_error: 0.0436 - val_loss: 0.5077 - val_mean_squared_error: 0.0438 - learning_rate: 1.0000e-05
Epoch 16/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 145s 496ms/step - loss: 0.5011 - mean_squared_error: 0.0367 - val_loss: 0.4921 - val_mean_squared_error: 0.0369 - learning_rate: 1.0000e-05
Epoch 17/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 146s 501ms/step - loss: 0.4868 - mean_squared_error: 0.0304 - val_loss: 0.4785 - val_mean_squared_error: 0.0311 - learning_rate: 1.0000e-05
Epoch 18/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 142s 485ms/step - loss: 0.4738 - mean_squared_error: 0.0247 - val_loss: 0.4654 - val_mean_squared_error: 0.0256 - learning_rate: 1.0000e-05
Epoch 19/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.4612 - mean_squared_error: 0.0201 - val_loss: 0.4515 - val_mean_squared_error: 0.0200 - learning_rate: 1.0000e-05
Epoch 20/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 473ms/step - loss: 0.4499 - mean_squared_error: 0.0160 - val_loss: 0.4439 - val_mean_squared_error: 0.0171 - learning_rate: 1.0000e-05
Epoch 21/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 469ms/step - loss: 0.4414 - mean_squared_error: 0.0124 - val_loss: 0.4351 - val_mean_squared_error: 0.0137 - learning_rate: 1.0000e-05
Epoch 22/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 469ms/step - loss: 0.4354 - mean_squared_error: 0.0095 - val_loss: 0.4283 - val_mean_squared_error: 0.0112 - learning_rate: 1.0000e-05
Epoch 23/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.4290 - mean_squared_error: 0.0071 - val_loss: 0.4227 - val_mean_squared_error: 0.0093 - learning_rate: 1.0000e-05
Epoch 24/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 139s 477ms/step - loss: 0.4218 - mean_squared_error: 0.0056 - val_loss: 0.4174 - val_mean_squared_error: 0.0075 - learning_rate: 1.0000e-05
Epoch 25/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 136s 466ms/step - loss: 0.4188 - mean_squared_error: 0.0041 - val_loss: 0.4146 - val_mean_squared_error: 0.0065 - learning_rate: 1.0000e-05
Epoch 26/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 136s 467ms/step - loss: 0.4148 - mean_squared_error: 0.0032 - val_loss: 0.4108 - val_mean_squared_error: 0.0053 - learning_rate: 1.0000e-05
Epoch 27/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 145s 496ms/step - loss: 0.4136 - mean_squared_error: 0.0025 - val_loss: 0.4082 - val_mean_squared_error: 0.0044 - learning_rate: 1.0000e-05
Epoch 28/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 154s 527ms/step - loss: 0.4110 - mean_squared_error: 0.0019 - val_loss: 0.4063 - val_mean_squared_error: 0.0038 - learning_rate: 1.0000e-05
Epoch 29/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 142s 487ms/step - loss: 0.4096 - mean_squared_error: 0.0016 - val_loss: 0.4058 - val_mean_squared_error: 0.0037 - learning_rate: 1.0000e-05
Epoch 30/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 470ms/step - loss: 0.4096 - mean_squared_error: 0.0013 - val_loss: 0.4050 - val_mean_squared_error: 0.0034 - learning_rate: 1.0000e-05
Epoch 31/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 473ms/step - loss: 0.4102 - mean_squared_error: 0.0012 - val_loss: 0.4044 - val_mean_squared_error: 0.0033 - learning_rate: 1.0000e-05
Epoch 32/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 474ms/step - loss: 0.4090 - mean_squared_error: 0.0011 - val_loss: 0.4040 - val_mean_squared_error: 0.0031 - learning_rate: 1.0000e-05
Epoch 33/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.4087 - mean_squared_error: 0.0010 - val_loss: 0.4033 - val_mean_squared_error: 0.0029 - learning_rate: 1.0000e-05
Epoch 34/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.4079 - mean_squared_error: 0.0010 - val_loss: 0.4037 - val_mean_squared_error: 0.0030 - learning_rate: 1.0000e-05
Epoch 35/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 142s 485ms/step - loss: 0.4109 - mean_squared_error: 9.6707e-04 - val_loss: 0.4032 - val_mean_squared_error: 0.0029 - learning_rate: 1.0000e-05
Epoch 36/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 153s 525ms/step - loss: 0.4092 - mean_squared_error: 9.3389e-04 - val_loss: 0.4035 - val_mean_squared_error: 0.0030 - learning_rate: 1.0000e-05
Epoch 37/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 154s 529ms/step - loss: 0.4071 - mean_squared_error: 9.4938e-04 - val_loss: 0.4025 - val_mean_squared_error: 0.0027 - learning_rate: 1.0000e-05
Epoch 38/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 143s 490ms/step - loss: 0.4065 - mean_squared_error: 9.0768e-04 - val_loss: 0.4027 - val_mean_squared_error: 0.0027 - learning_rate: 1.0000e-05
Epoch 39/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 470ms/step - loss: 0.4091 - mean_squared_error: 8.5881e-04 - val_loss: 0.4029 - val_mean_squared_error: 0.0028 - learning_rate: 1.0000e-05
Epoch 40/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 471ms/step - loss: 0.4084 - mean_squared_error: 8.5700e-04 - val_loss: 0.4027 - val_mean_squared_error: 0.0027 - learning_rate: 1.0000e-05
Epoch 41/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.4080 - mean_squared_error: 8.3285e-04 - val_loss: 0.4026 - val_mean_squared_error: 0.0028 - learning_rate: 1.0000e-05
Epoch 42/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.4066 - mean_squared_error: 8.5810e-04 - val_loss: 0.4024 - val_mean_squared_error: 0.0027 - learning_rate: 1.0000e-05
Epoch 43/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 471ms/step - loss: 0.4102 - mean_squared_error: 8.3282e-04 - val_loss: 0.4024 - val_mean_squared_error: 0.0027 - learning_rate: 1.0000e-05
Epoch 44/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 143s 490ms/step - loss: 0.4078 - mean_squared_error: 7.6995e-04 - val_loss: 0.4025 - val_mean_squared_error: 0.0027 - learning_rate: 1.0000e-05
Epoch 45/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 150s 515ms/step - loss: 0.4082 - mean_squared_error: 7.7627e-04 - val_loss: 0.4023 - val_mean_squared_error: 0.0026 - learning_rate: 1.0000e-05
Epoch 46/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 148s 507ms/step - loss: 0.4092 - mean_squared_error: 7.8152e-04 - val_loss: 0.4020 - val_mean_squared_error: 0.0026 - learning_rate: 1.0000e-05
Epoch 47/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 144s 492ms/step - loss: 0.4082 - mean_squared_error: 7.3046e-04 - val_loss: 0.4020 - val_mean_squared_error: 0.0026 - learning_rate: 1.0000e-05
Epoch 48/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 469ms/step - loss: 0.4087 - mean_squared_error: 7.4382e-04 - val_loss: 0.4021 - val_mean_squared_error: 0.0026 - learning_rate: 1.0000e-05
Epoch 49/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 470ms/step - loss: 0.4066 - mean_squared_error: 7.5448e-04 - val_loss: 0.4021 - val_mean_squared_error: 0.0026 - learning_rate: 1.0000e-05
Epoch 50/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 470ms/step - loss: 0.4072 - mean_squared_error: 7.7316e-04 - val_loss: 0.4020 - val_mean_squared_error: 0.0026 - learning_rate: 1.0000e-05
Epoch 51/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 473ms/step - loss: 0.4084 - mean_squared_error: 7.0784e-04 - val_loss: 0.4020 - val_mean_squared_error: 0.0025 - learning_rate: 1.0000e-05
Epoch 52/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 471ms/step - loss: 0.4087 - mean_squared_error: 7.3632e-04 - val_loss: 0.4020 - val_mean_squared_error: 0.0026 - learning_rate: 1.0000e-05
Epoch 53/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 142s 486ms/step - loss: 0.4063 - mean_squared_error: 7.1279e-04 - val_loss: 0.4020 - val_mean_squared_error: 0.0026 - learning_rate: 1.0000e-05
Epoch 54/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 145s 497ms/step - loss: 0.4082 - mean_squared_error: 6.9338e-04 - val_loss: 0.4017 - val_mean_squared_error: 0.0025 - learning_rate: 1.0000e-05
Epoch 55/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 149s 511ms/step - loss: 0.4068 - mean_squared_error: 6.9151e-04 - val_loss: 0.4017 - val_mean_squared_error: 0.0025 - learning_rate: 1.0000e-05
Epoch 56/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 141s 484ms/step - loss: 0.4070 - mean_squared_error: 6.7310e-04 - val_loss: 0.4021 - val_mean_squared_error: 0.0026 - learning_rate: 1.0000e-05
Epoch 57/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 470ms/step - loss: 0.4069 - mean_squared_error: 6.8701e-04 - val_loss: 0.4019 - val_mean_squared_error: 0.0025 - learning_rate: 1.0000e-05
Epoch 58/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.4067 - mean_squared_error: 7.1130e-04 - val_loss: 0.4019 - val_mean_squared_error: 0.0025 - learning_rate: 1.0000e-05
Epoch 59/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 469ms/step - loss: 0.4079 - mean_squared_error: 6.7344e-04 - val_loss: 0.4021 - val_mean_squared_error: 0.0026 - learning_rate: 1.0000e-05
Epoch 60/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 470ms/step - loss: 0.4085 - mean_squared_error: 6.8823e-04 - val_loss: 0.4016 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 61/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.4087 - mean_squared_error: 6.4379e-04 - val_loss: 0.4018 - val_mean_squared_error: 0.0025 - learning_rate: 1.0000e-05
Epoch 62/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 139s 476ms/step - loss: 0.4060 - mean_squared_error: 6.5046e-04 - val_loss: 0.4017 - val_mean_squared_error: 0.0025 - learning_rate: 1.0000e-05
Epoch 63/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.4051 - mean_squared_error: 6.1816e-04 - val_loss: 0.4016 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 64/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 136s 465ms/step - loss: 0.4089 - mean_squared_error: 6.1312e-04 - val_loss: 0.4016 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 65/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 142s 486ms/step - loss: 0.4068 - mean_squared_error: 6.4825e-04 - val_loss: 0.4014 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 66/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 151s 517ms/step - loss: 0.4057 - mean_squared_error: 6.1512e-04 - val_loss: 0.4015 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 67/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 155s 532ms/step - loss: 0.4075 - mean_squared_error: 6.2446e-04 - val_loss: 0.4015 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 68/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 136s 465ms/step - loss: 0.4074 - mean_squared_error: 5.9204e-04 - val_loss: 0.4014 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 69/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 136s 466ms/step - loss: 0.4068 - mean_squared_error: 6.0754e-04 - val_loss: 0.4015 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 70/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.4056 - mean_squared_error: 6.0360e-04 - val_loss: 0.4023 - val_mean_squared_error: 0.0027 - learning_rate: 1.0000e-05
Epoch 71/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 139s 475ms/step - loss: 0.4064 - mean_squared_error: 6.0216e-04 - val_loss: 0.4016 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 72/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 136s 467ms/step - loss: 0.4074 - mean_squared_error: 5.6818e-04 - val_loss: 0.4013 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-05
Epoch 73/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 469ms/step - loss: 0.4077 - mean_squared_error: 5.8116e-04 - val_loss: 0.4015 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 74/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 146s 500ms/step - loss: 0.4056 - mean_squared_error: 5.9187e-04 - val_loss: 0.4013 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-05
Epoch 75/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 150s 515ms/step - loss: 0.4066 - mean_squared_error: 5.6511e-04 - val_loss: 0.4013 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 76/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 147s 504ms/step - loss: 0.4078 - mean_squared_error: 5.5301e-04 - val_loss: 0.4015 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 77/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.4076 - mean_squared_error: 5.5795e-04 - val_loss: 0.4017 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 78/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 470ms/step - loss: 0.4045 - mean_squared_error: 5.5711e-04 - val_loss: 0.4013 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-05
Epoch 79/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 136s 465ms/step - loss: 0.4070 - mean_squared_error: 5.5179e-04 - val_loss: 0.4016 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 80/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 136s 465ms/step - loss: 0.4070 - mean_squared_error: 5.6309e-04 - val_loss: 0.4015 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 81/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 136s 466ms/step - loss: 0.4083 - mean_squared_error: 5.5748e-04 - val_loss: 0.4013 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-05
Epoch 82/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 140s 480ms/step - loss: 0.4079 - mean_squared_error: 5.1798e-04 - val_loss: 0.4014 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 83/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 144s 494ms/step - loss: 0.4055 - mean_squared_error: 5.5006e-04 - val_loss: 0.4015 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 84/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 0s 508ms/step - loss: 0.4075 - mean_squared_error: 5.0081e-04
Epoch 84: ReduceLROnPlateau reducing learning rate to 9.999999747378752e-07.
292/292 ━━━━━━━━━━━━━━━━━━━━ 150s 513ms/step - loss: 0.4075 - mean_squared_error: 5.0092e-04 - val_loss: 0.4016 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 85/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 144s 493ms/step - loss: 0.4071 - mean_squared_error: 5.4880e-04 - val_loss: 0.4013 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-06
Epoch 86/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 474ms/step - loss: 0.4065 - mean_squared_error: 5.2907e-04 - val_loss: 0.4013 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-06
Epoch 87/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 136s 466ms/step - loss: 0.4068 - mean_squared_error: 5.1186e-04 - val_loss: 0.4011 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-06
Epoch 88/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 136s 465ms/step - loss: 0.4057 - mean_squared_error: 5.3199e-04 - val_loss: 0.4013 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-06
Epoch 89/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 136s 466ms/step - loss: 0.4072 - mean_squared_error: 5.4235e-04 - val_loss: 0.4011 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-06
Epoch 90/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 469ms/step - loss: 0.4053 - mean_squared_error: 5.0030e-04 - val_loss: 0.4013 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-06
Epoch 91/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 140s 480ms/step - loss: 0.4060 - mean_squared_error: 5.1027e-04 - val_loss: 0.4011 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-06
Epoch 92/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 144s 493ms/step - loss: 0.4064 - mean_squared_error: 5.2571e-04 - val_loss: 0.4011 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-06
Epoch 93/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 144s 493ms/step - loss: 0.4065 - mean_squared_error: 5.3916e-04 - val_loss: 0.4013 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-06
Epoch 94/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 145s 497ms/step - loss: 0.4077 - mean_squared_error: 5.1107e-04 - val_loss: 0.4013 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-06
Epoch 95/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 143s 490ms/step - loss: 0.4085 - mean_squared_error: 5.0312e-04 - val_loss: 0.4013 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-06
Epoch 96/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 470ms/step - loss: 0.4053 - mean_squared_error: 4.9508e-04 - val_loss: 0.4011 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-06
Epoch 97/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 0s 467ms/step - loss: 0.4073 - mean_squared_error: 4.9562e-04
Epoch 97: ReduceLROnPlateau reducing learning rate to 1e-07.
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 474ms/step - loss: 0.4073 - mean_squared_error: 4.9570e-04 - val_loss: 0.4010 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-06
Epoch 98/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 139s 474ms/step - loss: 0.4071 - mean_squared_error: 5.2952e-04 - val_loss: 0.4010 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-07
Epoch 99/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 474ms/step - loss: 0.4060 - mean_squared_error: 4.8378e-04 - val_loss: 0.4012 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-07
Epoch 100/100
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 474ms/step - loss: 0.4075 - mean_squared_error: 5.2382e-04 - val_loss: 0.4011 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-07
Restoring model weights from the end of the best epoch: 97.

In [8]:

## LOAD CHECKPOINTS IF NEEDED
# 

# Load the model
model = load_model('smogseer100.keras')

# Run predictions on validation data
predictions = model.predict(X_val)

# Evaluate the model on validation data
val_loss, val_accuracy = model.evaluate(X_val, y_val)
print(f"Validation Loss: {val_loss}")
print(f"Validation Accuracy: {val_accuracy}")

3/3 ━━━━━━━━━━━━━━━━━━━━ 6s 814ms/step
3/3 ━━━━━━━━━━━━━━━━━━━━ 3s 456ms/step - loss: 0.4003 - mean_squared_error: 0.0019
Validation Loss: 0.40102294087409973
Validation Accuracy: 0.0022550118155777454

In [9]:

# Plot comparisons and training history

def plot_comparison(y_true, y_pred, index, save_path):
    """
    Plots the ground truth and the predicted output for a given index.
    
    Parameters:
    - y_true: Ground truth data
    - y_pred: Predicted data
    - index: Index of the sample to plot
    - save_path: Path to save the plot
    """
    fig, axes = plt.subplots(1, 2, figsize=(12, 6))

    # Plot ground truth
    ax = axes[0]
    ax.imshow(y_true[index, 0, :, :, 0], cmap='viridis')
    ax.set_title('Ground Truth')
    ax.axis('off')

    # Plot prediction
    ax = axes[1]
    ax.imshow(y_pred[index, 0, :, :, 0], cmap='viridis')
    ax.set_title('Prediction')
    ax.axis('off')

    plt.tight_layout()
    plt.savefig(save_path)
    plt.close()

# Visualize a few samples
num_samples_to_plot = 5
for i in range(num_samples_to_plot):
    plot_comparison(y_val, predictions, i, f'comparison_plot_100_{i}.png')

# Plot training history
def plot_training_history(history, save_path):
    """
    Plots the training and validation loss and accuracy over epochs.

    Parameters:
    - history: Keras History object
    - save_path: Path to save the plot
    """
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

    # Plot loss
    ax1.plot(history.history['loss'], label='Training Loss')
    ax1.plot(history.history['val_loss'], label='Validation Loss')
    ax1.set_title('Loss over epochs')
    ax1.set_xlabel('Epoch')
    ax1.set_ylabel('Loss')
    ax1.legend()

    # Plot accuracy
    ax2.plot(history.history['mean_squared_error'], label='Training MSE')
    ax2.plot(history.history['val_mean_squared_error'], label='Validation MSE')
    ax2.set_title('MSE over epochs')
    ax2.set_xlabel('Epoch')
    ax2.set_ylabel('MSE')
    ax2.legend()

    plt.tight_layout()
    plt.savefig(save_path)
    plt.close()

# Plot training history
plot_training_history(history, 'training_history_epoch100.png')