Smogseer training at 50 epochs

In [20]:

import matplotlib.pyplot as plt
import xarray as xr
import numpy as np
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.impute import SimpleImputer
from tensorflow.keras.models import load_model
import matplotlib.pyplot as plt
from tensorflow.keras.utils import Sequence

In [21]:

# Load your dataset
ds = xr.open_dataset('S5PL2_5D.nc')
ds

<xarray.Dataset> Size: 2GB
Dimensions:         (time: 366, lat: 291, lon: 512, bnds: 2)
Coordinates:
  * lat             (lat) float64 2kB 34.36 34.33 34.3 ... 24.97 24.94 24.9
  * lon             (lon) float64 4kB 68.15 68.19 68.22 ... 84.75 84.79 84.82
  * time            (time) datetime64[ns] 3kB 2019-01-03T12:00:00 ... 2024-01...
    time_bnds       (time, bnds) datetime64[ns] 6kB ...
Dimensions without coordinates: bnds
Data variables:
    AER_AI_340_380  (time, lat, lon) float32 218MB ...
    AER_AI_354_388  (time, lat, lon) float32 218MB ...
    CH4             (time, lat, lon) float32 218MB ...
    CLOUD_FRACTION  (time, lat, lon) float32 218MB ...
    CO              (time, lat, lon) float32 218MB ...
    HCHO            (time, lat, lon) float32 218MB ...
    NO2             (time, lat, lon) float32 218MB ...
    O3              (time, lat, lon) float32 218MB ...
    SO2             (time, lat, lon) float32 218MB ...
Attributes:
    Conventions:               CF-1.7
    title:                     S5PL2 Data Cube Subset
    history:                   [{'program': 'xcube_sh.chunkstore.SentinelHubC...
    date_created:              2024-05-02T13:00:01.155492
    time_coverage_start:       2019-01-01T00:00:00+00:00
    time_coverage_end:         2024-01-05T00:00:00+00:00
    time_coverage_duration:    P1830DT0H0M0S
    time_coverage_resolution:  P5DT0H0M0S
    geospatial_lon_min:        68.137207
    geospatial_lat_min:        24.886436
    geospatial_lon_max:        84.836426
    geospatial_lat_max:        34.37759367382812

xarray.Dataset

• Dimensions:
  • time: 366
  • lat: 291
  • lon: 512
  • bnds: 2
• Coordinates: (4)
  • lat
    (lat)
    float64
    34.36 34.33 34.3 ... 24.94 24.9

    units :

    decimal_degrees

    long_name :

    latitude

    standard_name :

    latitude

    array([34.361286, 34.32867 , 34.296055, ..., 24.967975, 24.935359, 24.902744])

  • lon
    (lon)
    float64
    68.15 68.19 68.22 ... 84.79 84.82

    units :

    decimal_degrees

    long_name :

    longitude

    standard_name :

    longitude

    array([68.153515, 68.18613 , 68.218746, ..., 84.754887, 84.787503, 84.820118])

  • time
    (time)
    datetime64[ns]
    2019-01-03T12:00:00 ... 2024-01-...

    standard_name :

    time

    bounds :

    time_bnds

    array(['2019-01-03T12:00:00.000000000', '2019-01-08T12:00:00.000000000',
           '2019-01-13T12:00:00.000000000', ..., '2023-12-23T12:00:00.000000000',
           '2023-12-28T12:00:00.000000000', '2024-01-02T12:00:00.000000000'],
          dtype='datetime64[ns]')

  • time_bnds
    (time, bnds)
    datetime64[ns]
    ...

    [732 values with dtype=datetime64[ns]]

• Data variables: (9)
  • AER_AI_340_380
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    Unitless

    [54531072 values with dtype=float32]

  • AER_AI_354_388
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    Unitless

    [54531072 values with dtype=float32]

  • CH4
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    parts per billion

    [54531072 values with dtype=float32]

  • CLOUD_FRACTION
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    Unitless

    [54531072 values with dtype=float32]

  • CO
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    mol/m^2

    [54531072 values with dtype=float32]

  • HCHO
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    mol/m^2

    [54531072 values with dtype=float32]

  • NO2
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    mol/m^2

    [54531072 values with dtype=float32]

  • O3
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    mol/m^2

    [54531072 values with dtype=float32]

  • SO2
    (time, lat, lon)
    float32
    ...

    sample_type :

    FLOAT32

    units :

    mol/m^2

    [54531072 values with dtype=float32]

• Indexes: (3)
  • lat
    PandasIndex

    PandasIndex(Index([34.361285842773434,  34.32867018066406,  34.29605451855468,
            34.26343885644531,  34.23082319433593,  34.19820753222656,
            34.16559187011718,  34.13297620800781,  34.10036054589843,
            34.06774488378906,
           ...
            25.19628479003906, 25.163669127929687,  25.13105346582031,
           25.098437803710937,  25.06582214160156, 25.033206479492186,
            25.00059081738281, 24.967975155273436,  24.93535949316406,
           24.902743831054686],
          dtype='float64', name='lat', length=291))

  • lon
    PandasIndex

    PandasIndex(Index([ 68.1535148310547, 68.18613049316407, 68.21874615527344,
           68.25136181738281,  68.2839774794922, 68.31659314160157,
           68.34920880371094, 68.38182446582032,  68.4144401279297,
           68.44705579003907,
           ...
           84.52657720996093, 84.55919287207031, 84.59180853417969,
           84.62442419628906, 84.65703985839843, 84.68965552050781,
           84.72227118261719, 84.75488684472657, 84.78750250683593,
           84.82011816894531],
          dtype='float64', name='lon', length=512))

  • time
    PandasIndex

    PandasIndex(DatetimeIndex(['2019-01-03 12:00:00', '2019-01-08 12:00:00',
                   '2019-01-13 12:00:00', '2019-01-18 12:00:00',
                   '2019-01-23 12:00:00', '2019-01-28 12:00:00',
                   '2019-02-02 12:00:00', '2019-02-07 12:00:00',
                   '2019-02-12 12:00:00', '2019-02-17 12:00:00',
                   ...
                   '2023-11-18 12:00:00', '2023-11-23 12:00:00',
                   '2023-11-28 12:00:00', '2023-12-03 12:00:00',
                   '2023-12-08 12:00:00', '2023-12-13 12:00:00',
                   '2023-12-18 12:00:00', '2023-12-23 12:00:00',
                   '2023-12-28 12:00:00', '2024-01-02 12:00:00'],
                  dtype='datetime64[ns]', name='time', length=366, freq=None))

• Attributes: (12)

  Conventions :

  CF-1.7

  title :

  S5PL2 Data Cube Subset

  history :

  [{'program': 'xcube_sh.chunkstore.SentinelHubChunkStore', 'cube_config': {'dataset_name': 'S5PL2', 'band_names': ['NO2', 'SO2', 'O3', 'CO', 'CH4', 'HCHO', 'AER_AI_340_380', 'AER_AI_354_388', 'CLOUD_FRACTION'], 'band_fill_values': None, 'band_sample_types': None, 'band_units': None, 'tile_size': [512, 291], 'bbox': [68.137207, 24.886436, 84.836426, 34.37759367382812], 'spatial_res': 0.032615662109375, 'crs': 'WGS84', 'upsampling': 'BILINEAR', 'downsampling': 'NEAREST', 'mosaicking_order': 'mostRecent', 'time_range': ['2019-01-01T00:00:00+00:00', '2023-12-31T00:00:00+00:00'], 'time_period': '5 days 00:00:00', 'time_tolerance': None, 'collection_id': None, 'four_d': False}}]

  date_created :

  2024-05-02T13:00:01.155492

  time_coverage_start :

  2019-01-01T00:00:00+00:00

  time_coverage_end :

  2024-01-05T00:00:00+00:00

  time_coverage_duration :

  P1830DT0H0M0S

  time_coverage_resolution :

  P5DT0H0M0S

  geospatial_lon_min :

  68.137207

  geospatial_lat_min :

  24.886436

  geospatial_lon_max :

  84.836426

  geospatial_lat_max :

  34.37759367382812

In [23]:

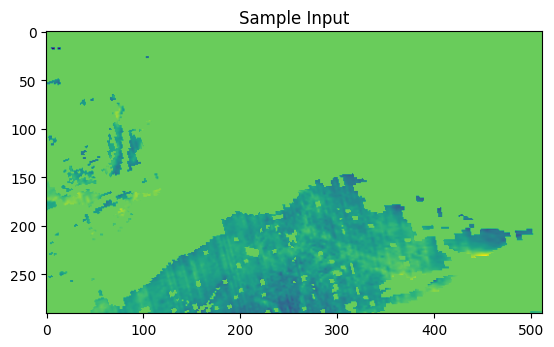
# Stack the features into a single DataArray
features = ['SO2', 'NO2', 'CH4', 'O3', 'CO', 'HCHO']
data = xr.concat([ds[feature] for feature in features], dim='feature')
data = data.transpose('time', 'lat', 'lon', 'feature')

# Convert to NumPy arrays
X_data = data.values.astype(np.float32)

# Normalize the input data
scaler = StandardScaler()
X_data = scaler.fit_transform(X_data.reshape(-1, X_data.shape[-1])).reshape(X_data.shape)

# Impute nan values with the mean of the respective feature
X_data_reshaped = X_data.reshape(-1, X_data.shape[-1])
imputer = SimpleImputer(strategy='mean')
X_data_imputed = imputer.fit_transform(X_data_reshaped)
X_data_imputed = X_data_imputed.reshape(X_data.shape)

# Add the time dimension to the input data
X_data_imputed = np.expand_dims(X_data_imputed, axis=1)

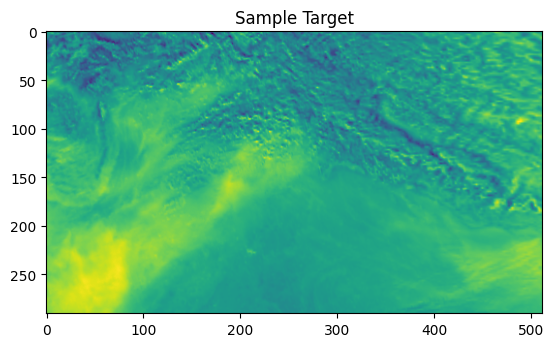
# Load your actual target data
ds_target = xr.open_dataset('S5PL2_5D.nc')
target_data = ds_target['AER_AI_340_380'].values.astype(np.float32)

# Normalize target data to [0, 1]
target_scaler = MinMaxScaler()
target_data = target_scaler.fit_transform(target_data.reshape(-1, 1)).reshape(target_data.shape)

# Impute nan values in target data
target_data_reshaped = target_data.reshape(-1, target_data.shape[-1])
target_data_imputed = imputer.fit_transform(target_data_reshaped)
target_data_imputed = target_data_imputed.reshape(target_data.shape)

# Ensure the target data shape is (num_samples, num_timesteps, num_latitudes, num_longitudes, 1)
target_data_imputed = target_data_imputed.reshape((target_data.shape[0], 1, target_data.shape[1], target_data.shape[2], 1))

# Remove samples with nan values in target data
non_nan_target_indices = ~np.isnan(target_data_imputed).any(axis=(1, 2, 3, 4))
X_data_clean = X_data_imputed[non_nan_target_indices]
y_data_clean = target_data_imputed[non_nan_target_indices]

# Ensure target values are within the valid range [0, 1]
print("Target data range: ", y_data_clean.max(), y_data_clean.min())

# Split data into training and validation sets
split_ratio = 0.8
split_idx = int(split_ratio * X_data_clean.shape[0])

X_train, X_val = X_data_clean[:split_idx], X_data_clean[split_idx:]
y_train, y_val = y_data_clean[:split_idx], y_data_clean[split_idx:]

Target data range:  1.0 0.0

In [19]:

print("Input shape:", X_data_clean.shape)
print("Target shape:", y_data_clean.shape)
print("Max and Min of Target Data:", y_data_clean.max(), y_data_clean.min())

Input shape: (366, 1, 291, 512, 6)
Target shape: (366, 1, 291, 512, 1)
Max and Min of Target Data: 1.0 0.0

In [20]:

print("Training data shape:", X_train.shape)
print("Validation data shape:", X_val.shape)
print("Training target shape:", y_train.shape)
print("Validation target shape:", y_val.shape)

Training data shape: (292, 1, 291, 512, 6)
Validation data shape: (74, 1, 291, 512, 6)
Training target shape: (292, 1, 291, 512, 1)
Validation target shape: (74, 1, 291, 512, 1)

In [21]:

import matplotlib.pyplot as plt

# Visualize a sample from the training data
sample_index = 0
plt.imshow(X_train[sample_index, 0, :, :, 2], cmap='viridis')
plt.title('Sample Input')
plt.show()

plt.imshow(y_train[sample_index, 0, :, :, 0], cmap='viridis')
plt.title('Sample Target')
plt.show()

In [31]:

np.save("X_val.npy", X_val)
np.save("Y_val.npy", y_val)

In [23]:

# Define the model with correct input shape
inp = layers.Input(shape=(1, X_data_clean.shape[2], X_data_clean.shape[3], X_data_clean.shape[4]))

x = layers.BatchNormalization()(inp)
x = layers.ConvLSTM2D(
    filters=16,
    kernel_size=(3, 3),
    padding="same",
    return_sequences=True,
    activation="tanh",
    recurrent_activation="sigmoid",
    kernel_initializer="glorot_uniform"
)(x)
x = layers.BatchNormalization()(x)
x = layers.ConvLSTM2D(
    filters=32,
    kernel_size=(3, 3),
    padding="same",
    return_sequences=True,
    activation="tanh",
    recurrent_activation="sigmoid",
    kernel_initializer="glorot_uniform"
)(x)
x = layers.BatchNormalization()(x)
x = layers.Conv3D(
    filters=1, kernel_size=(3, 3, 3), activation="sigmoid", padding="same"
)(x)

model = keras.models.Model(inp, x, name="smogseer")

# Use a reduced learning rate and gradient clipping
optimizer = keras.optimizers.Adam(learning_rate=1e-5, clipnorm=1.0)
model.compile(
    loss=keras.losses.binary_crossentropy,
    optimizer=optimizer,
    metrics=['mean_squared_error']
)

# Print the model summary
model.summary()

# Data Generator Class

class DataGenerator(Sequence):
    def __init__(self, X_data, y_data, batch_size):
        self.X_data = X_data
        self.y_data = y_data
        self.batch_size = batch_size
        self.indices = np.arange(X_data.shape[0])
        
    def __len__(self):
        return int(np.ceil(len(self.indices) / self.batch_size))
    
    def __getitem__(self, index):
        batch_indices = self.indices[index * self.batch_size:(index + 1) * self.batch_size]
        batch_X = self.X_data[batch_indices]
        batch_y = self.y_data[batch_indices]
        return batch_X, batch_y

    def on_epoch_end(self):
        np.random.shuffle(self.indices)

batch_size = 1
train_generator = DataGenerator(X_train, y_train, batch_size)
val_generator = DataGenerator(X_val, y_val, batch_size)

# Define callbacks for monitoring and adjusting learning rate
callbacks = [
    keras.callbacks.ReduceLROnPlateau(
        monitor='val_loss', factor=0.1, patience=10, verbose=1, min_lr=1e-7
    ),
    keras.callbacks.EarlyStopping(
        monitor='val_loss', patience=15, verbose=1, restore_best_weights=True
    ),
    keras.callbacks.TensorBoard(log_dir='./logs')
]

# Train the model using data generators
history = model.fit(train_generator, epochs=50, validation_data=val_generator, callbacks=callbacks)
# Save the model
model.save('smogseer.keras')

Model: "smogseer"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ input_layer_1 (InputLayer)      │ (None, 1, 291, 512, 6) │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ batch_normalization_3           │ (None, 1, 291, 512, 6) │            24 │
│ (BatchNormalization)            │                        │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv_lstm2d_2 (ConvLSTM2D)      │ (None, 1, 291, 512,    │        12,736 │
│                                 │ 16)                    │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ batch_normalization_4           │ (None, 1, 291, 512,    │            64 │
│ (BatchNormalization)            │ 16)                    │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv_lstm2d_3 (ConvLSTM2D)      │ (None, 1, 291, 512,    │        55,424 │
│                                 │ 32)                    │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ batch_normalization_5           │ (None, 1, 291, 512,    │           128 │
│ (BatchNormalization)            │ 32)                    │               │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv3d_1 (Conv3D)               │ (None, 1, 291, 512, 1) │           865 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

 Total params: 69,241 (270.47 KB)

 Trainable params: 69,133 (270.05 KB)

 Non-trainable params: 108 (432.00 B)

Epoch 1/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 150s 496ms/step - loss: 0.7337 - mean_squared_error: 0.1448 - val_loss: 0.6862 - val_mean_squared_error: 0.1305 - learning_rate: 1.0000e-05
Epoch 2/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 469ms/step - loss: 0.7032 - mean_squared_error: 0.1331 - val_loss: 0.6964 - val_mean_squared_error: 0.1351 - learning_rate: 1.0000e-05
Epoch 3/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 473ms/step - loss: 0.6931 - mean_squared_error: 0.1289 - val_loss: 0.7002 - val_mean_squared_error: 0.1363 - learning_rate: 1.0000e-05
Epoch 4/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.6858 - mean_squared_error: 0.1247 - val_loss: 0.6941 - val_mean_squared_error: 0.1334 - learning_rate: 1.0000e-05
Epoch 5/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 473ms/step - loss: 0.6783 - mean_squared_error: 0.1212 - val_loss: 0.6801 - val_mean_squared_error: 0.1267 - learning_rate: 1.0000e-05
Epoch 6/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 139s 478ms/step - loss: 0.6691 - mean_squared_error: 0.1169 - val_loss: 0.6731 - val_mean_squared_error: 0.1232 - learning_rate: 1.0000e-05
Epoch 7/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 141s 483ms/step - loss: 0.6576 - mean_squared_error: 0.1122 - val_loss: 0.6551 - val_mean_squared_error: 0.1144 - learning_rate: 1.0000e-05
Epoch 8/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 147s 503ms/step - loss: 0.6441 - mean_squared_error: 0.1054 - val_loss: 0.6403 - val_mean_squared_error: 0.1071 - learning_rate: 1.0000e-05
Epoch 9/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 149s 510ms/step - loss: 0.6289 - mean_squared_error: 0.0970 - val_loss: 0.6240 - val_mean_squared_error: 0.0991 - learning_rate: 1.0000e-05
Epoch 10/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 144s 492ms/step - loss: 0.6117 - mean_squared_error: 0.0892 - val_loss: 0.6035 - val_mean_squared_error: 0.0891 - learning_rate: 1.0000e-05
Epoch 11/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 142s 485ms/step - loss: 0.5937 - mean_squared_error: 0.0801 - val_loss: 0.5833 - val_mean_squared_error: 0.0794 - learning_rate: 1.0000e-05
Epoch 12/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 469ms/step - loss: 0.5754 - mean_squared_error: 0.0714 - val_loss: 0.5642 - val_mean_squared_error: 0.0702 - learning_rate: 1.0000e-05
Epoch 13/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.5567 - mean_squared_error: 0.0626 - val_loss: 0.5496 - val_mean_squared_error: 0.0634 - learning_rate: 1.0000e-05
Epoch 14/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 473ms/step - loss: 0.5387 - mean_squared_error: 0.0540 - val_loss: 0.5301 - val_mean_squared_error: 0.0543 - learning_rate: 1.0000e-05
Epoch 15/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 469ms/step - loss: 0.5220 - mean_squared_error: 0.0461 - val_loss: 0.5103 - val_mean_squared_error: 0.0453 - learning_rate: 1.0000e-05
Epoch 16/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 142s 486ms/step - loss: 0.5051 - mean_squared_error: 0.0391 - val_loss: 0.4963 - val_mean_squared_error: 0.0390 - learning_rate: 1.0000e-05
Epoch 17/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 147s 503ms/step - loss: 0.4907 - mean_squared_error: 0.0324 - val_loss: 0.4815 - val_mean_squared_error: 0.0326 - learning_rate: 1.0000e-05
Epoch 18/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 147s 502ms/step - loss: 0.4774 - mean_squared_error: 0.0263 - val_loss: 0.4664 - val_mean_squared_error: 0.0263 - learning_rate: 1.0000e-05
Epoch 19/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 146s 501ms/step - loss: 0.4648 - mean_squared_error: 0.0214 - val_loss: 0.4584 - val_mean_squared_error: 0.0230 - learning_rate: 1.0000e-05
Epoch 20/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 142s 485ms/step - loss: 0.4539 - mean_squared_error: 0.0169 - val_loss: 0.4452 - val_mean_squared_error: 0.0177 - learning_rate: 1.0000e-05
Epoch 21/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 139s 475ms/step - loss: 0.4444 - mean_squared_error: 0.0133 - val_loss: 0.4366 - val_mean_squared_error: 0.0144 - learning_rate: 1.0000e-05
Epoch 22/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.4362 - mean_squared_error: 0.0103 - val_loss: 0.4267 - val_mean_squared_error: 0.0108 - learning_rate: 1.0000e-05
Epoch 23/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 473ms/step - loss: 0.4303 - mean_squared_error: 0.0077 - val_loss: 0.4232 - val_mean_squared_error: 0.0096 - learning_rate: 1.0000e-05
Epoch 24/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 139s 475ms/step - loss: 0.4241 - mean_squared_error: 0.0058 - val_loss: 0.4167 - val_mean_squared_error: 0.0073 - learning_rate: 1.0000e-05
Epoch 25/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 145s 497ms/step - loss: 0.4207 - mean_squared_error: 0.0044 - val_loss: 0.4112 - val_mean_squared_error: 0.0054 - learning_rate: 1.0000e-05
Epoch 26/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 147s 502ms/step - loss: 0.4154 - mean_squared_error: 0.0034 - val_loss: 0.4105 - val_mean_squared_error: 0.0052 - learning_rate: 1.0000e-05
Epoch 27/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 146s 499ms/step - loss: 0.4136 - mean_squared_error: 0.0026 - val_loss: 0.4066 - val_mean_squared_error: 0.0040 - learning_rate: 1.0000e-05
Epoch 28/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 146s 500ms/step - loss: 0.4119 - mean_squared_error: 0.0020 - val_loss: 0.4046 - val_mean_squared_error: 0.0033 - learning_rate: 1.0000e-05
Epoch 29/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 139s 476ms/step - loss: 0.4105 - mean_squared_error: 0.0016 - val_loss: 0.4034 - val_mean_squared_error: 0.0030 - learning_rate: 1.0000e-05
Epoch 30/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 474ms/step - loss: 0.4106 - mean_squared_error: 0.0013 - val_loss: 0.4030 - val_mean_squared_error: 0.0029 - learning_rate: 1.0000e-05
Epoch 31/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.4078 - mean_squared_error: 0.0012 - val_loss: 0.4021 - val_mean_squared_error: 0.0026 - learning_rate: 1.0000e-05
Epoch 32/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 471ms/step - loss: 0.4087 - mean_squared_error: 0.0011 - val_loss: 0.4015 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 33/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 139s 475ms/step - loss: 0.4083 - mean_squared_error: 9.7096e-04 - val_loss: 0.4016 - val_mean_squared_error: 0.0024 - learning_rate: 1.0000e-05
Epoch 34/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 141s 483ms/step - loss: 0.4075 - mean_squared_error: 9.5572e-04 - val_loss: 0.4013 - val_mean_squared_error: 0.0023 - learning_rate: 1.0000e-05
Epoch 35/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 139s 475ms/step - loss: 0.4084 - mean_squared_error: 9.2558e-04 - val_loss: 0.4006 - val_mean_squared_error: 0.0021 - learning_rate: 1.0000e-05
Epoch 36/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 137s 469ms/step - loss: 0.4088 - mean_squared_error: 8.9947e-04 - val_loss: 0.4008 - val_mean_squared_error: 0.0022 - learning_rate: 1.0000e-05
Epoch 37/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 139s 477ms/step - loss: 0.4081 - mean_squared_error: 8.2714e-04 - val_loss: 0.4005 - val_mean_squared_error: 0.0021 - learning_rate: 1.0000e-05
Epoch 38/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 147s 504ms/step - loss: 0.4093 - mean_squared_error: 8.5030e-04 - val_loss: 0.4005 - val_mean_squared_error: 0.0021 - learning_rate: 1.0000e-05
Epoch 39/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 146s 500ms/step - loss: 0.4090 - mean_squared_error: 8.4955e-04 - val_loss: 0.4002 - val_mean_squared_error: 0.0020 - learning_rate: 1.0000e-05
Epoch 40/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 148s 507ms/step - loss: 0.4085 - mean_squared_error: 8.1096e-04 - val_loss: 0.4000 - val_mean_squared_error: 0.0019 - learning_rate: 1.0000e-05
Epoch 41/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 140s 481ms/step - loss: 0.4082 - mean_squared_error: 7.9257e-04 - val_loss: 0.4003 - val_mean_squared_error: 0.0020 - learning_rate: 1.0000e-05
Epoch 42/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 473ms/step - loss: 0.4087 - mean_squared_error: 7.7913e-04 - val_loss: 0.4006 - val_mean_squared_error: 0.0021 - learning_rate: 1.0000e-05
Epoch 43/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 139s 474ms/step - loss: 0.4088 - mean_squared_error: 7.6459e-04 - val_loss: 0.3999 - val_mean_squared_error: 0.0019 - learning_rate: 1.0000e-05
Epoch 44/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 473ms/step - loss: 0.4083 - mean_squared_error: 7.5364e-04 - val_loss: 0.4001 - val_mean_squared_error: 0.0020 - learning_rate: 1.0000e-05
Epoch 45/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 473ms/step - loss: 0.4066 - mean_squared_error: 7.8711e-04 - val_loss: 0.3999 - val_mean_squared_error: 0.0019 - learning_rate: 1.0000e-05
Epoch 46/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 145s 495ms/step - loss: 0.4093 - mean_squared_error: 7.6262e-04 - val_loss: 0.3998 - val_mean_squared_error: 0.0019 - learning_rate: 1.0000e-05
Epoch 47/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 147s 504ms/step - loss: 0.4076 - mean_squared_error: 7.3529e-04 - val_loss: 0.3997 - val_mean_squared_error: 0.0019 - learning_rate: 1.0000e-05
Epoch 48/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 145s 496ms/step - loss: 0.4094 - mean_squared_error: 6.9850e-04 - val_loss: 0.3998 - val_mean_squared_error: 0.0019 - learning_rate: 1.0000e-05
Epoch 49/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 147s 503ms/step - loss: 0.4087 - mean_squared_error: 7.1750e-04 - val_loss: 0.3997 - val_mean_squared_error: 0.0019 - learning_rate: 1.0000e-05
Epoch 50/50
292/292 ━━━━━━━━━━━━━━━━━━━━ 138s 472ms/step - loss: 0.4070 - mean_squared_error: 6.8971e-04 - val_loss: 0.3996 - val_mean_squared_error: 0.0018 - learning_rate: 1.0000e-05
Restoring model weights from the end of the best epoch: 50.

In [6]:

## LOAD CHECKPOINTS IF NEEDED
X_val = np.load('X_val.npy')
y_val = np.load('Y_val.npy')

# Load the model
model = load_model('smogseer50.keras')

# Run predictions on validation data
predictions = model.predict(X_val)

# Evaluate the model on validation data
val_loss, val_accuracy = model.evaluate(X_val, y_val)
print(f"Validation Loss: {val_loss}")
print(f"Validation Accuracy: {val_accuracy}")

3/3 ━━━━━━━━━━━━━━━━━━━━ 7s 747ms/step
3/3 ━━━━━━━━━━━━━━━━━━━━ 3s 460ms/step - loss: 0.3992 - mean_squared_error: 0.0016
Validation Loss: 0.39958614110946655
Validation Accuracy: 0.0018263210076838732

In [28]:

# Plot comparisons and training history

def plot_comparison(y_true, y_pred, index, save_path):
    """
    Plots the ground truth and the predicted output for a given index.
    
    Parameters:
    - y_true: Ground truth data
    - y_pred: Predicted data
    - index: Index of the sample to plot
    - save_path: Path to save the plot
    """
    fig, axes = plt.subplots(1, 2, figsize=(12, 6))

    # Plot ground truth
    ax = axes[0]
    ax.imshow(y_true[index, 0, :, :, 0], cmap='viridis')
    ax.set_title('Ground Truth')
    ax.axis('off')

    # Plot prediction
    ax = axes[1]
    ax.imshow(y_pred[index, 0, :, :, 0], cmap='viridis')
    ax.set_title('Prediction')
    ax.axis('off')

    plt.tight_layout()
    plt.savefig(save_path)
    plt.close()

# Visualize a few samples
num_samples_to_plot = 5
for i in range(num_samples_to_plot):
    plot_comparison(y_val, predictions, i, f'comparison_plot_{i}.png')

# Plot training history
def plot_training_history(history, save_path):
    """
    Plots the training and validation loss and accuracy over epochs.

    Parameters:
    - history: Keras History object
    - save_path: Path to save the plot
    """
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

    # Plot loss
    ax1.plot(history.history['loss'], label='Training Loss')
    ax1.plot(history.history['val_loss'], label='Validation Loss')
    ax1.set_title('Loss over epochs')
    ax1.set_xlabel('Epoch')
    ax1.set_ylabel('Loss')
    ax1.legend()

    # Plot accuracy
    ax2.plot(history.history['mean_squared_error'], label='Training MSE')
    ax2.plot(history.history['val_mean_squared_error'], label='Validation MSE')
    ax2.set_title('MSE over epochs')
    ax2.set_xlabel('Epoch')
    ax2.set_ylabel('MSE')
    ax2.legend()

    plt.tight_layout()
    plt.savefig(save_path)
    plt.close()

# Plot training history
plot_training_history(history, 'training_history_epoch50.png')

In [24]:

# Visualize a few samples
num_timesteps_to_plot = 5
for i in range(num_timesteps_to_plot):
    print(predictions[i, 0, :, :, 0].shape)

(291, 512)
(291, 512)
(291, 512)
(291, 512)
(291, 512)

In [25]:

print("Target data range: ", predictions.max(), predictions.min())

Target data range:  0.99998665 1.6277676e-06